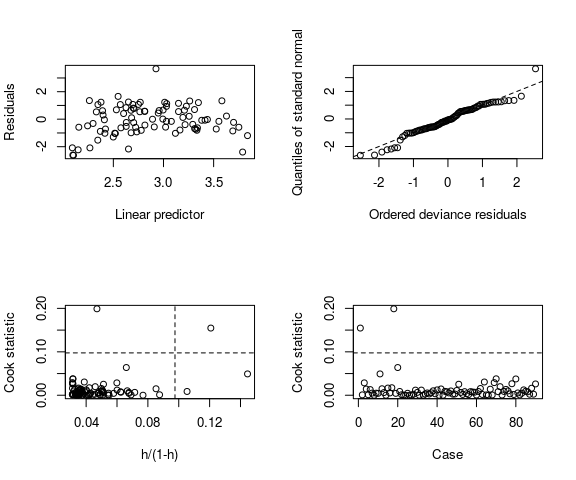
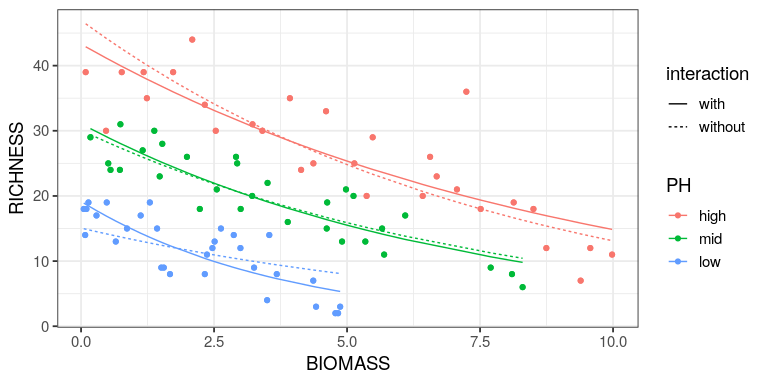
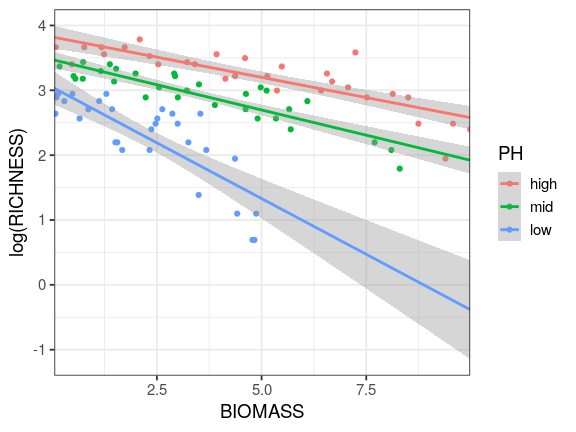
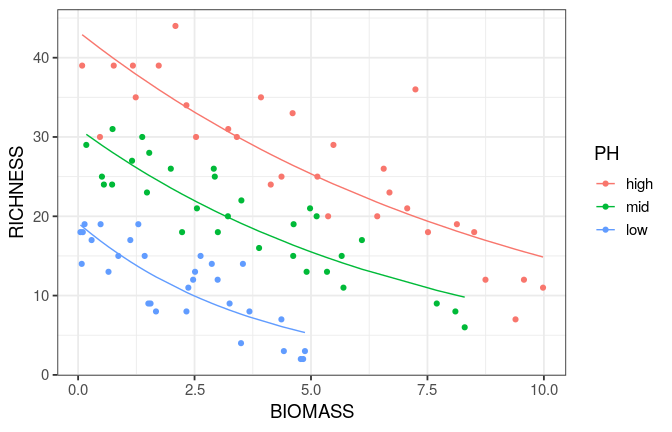
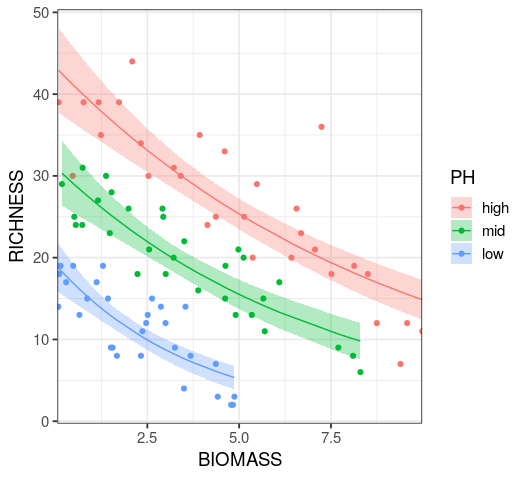
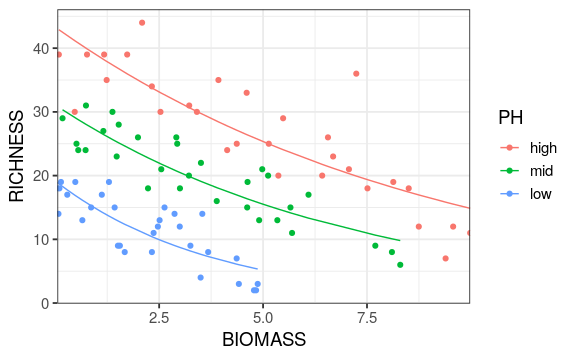
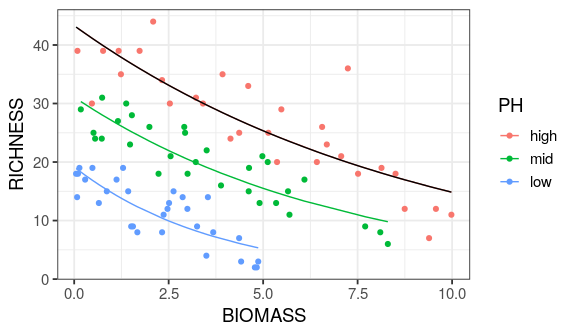
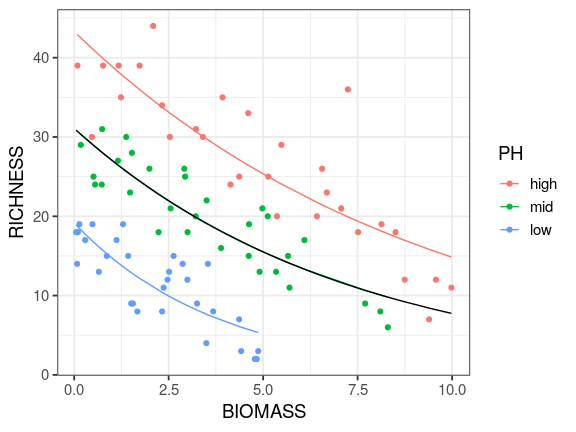
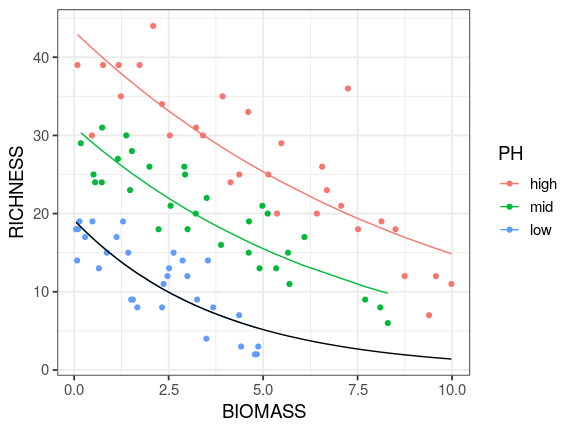
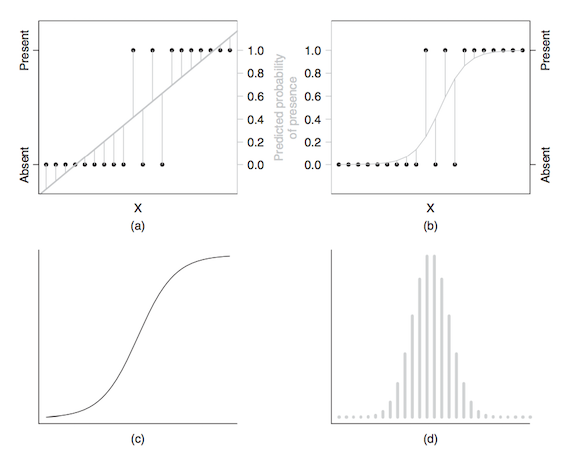
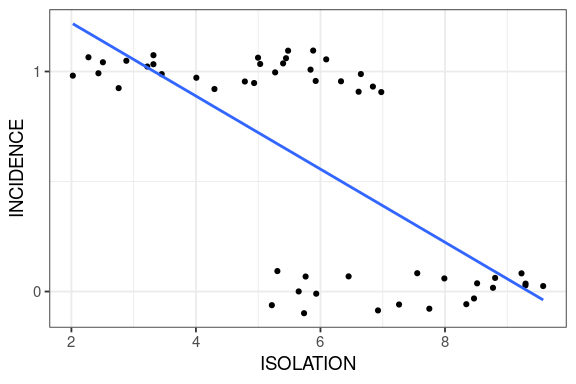
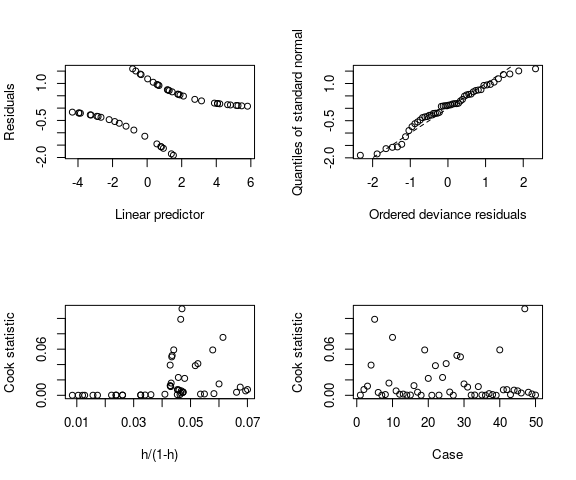
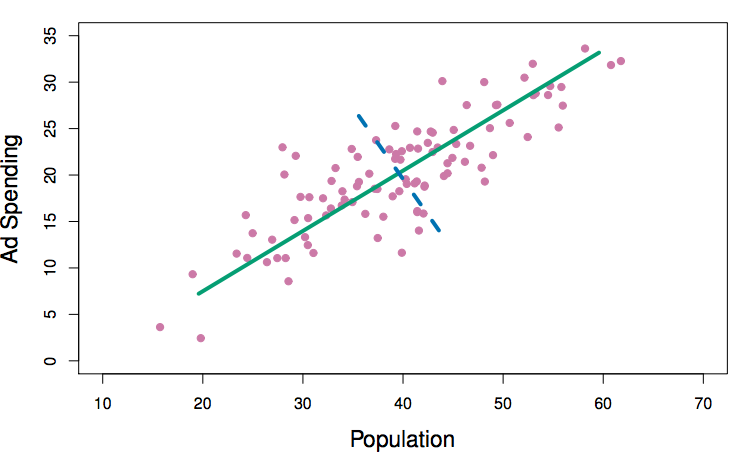
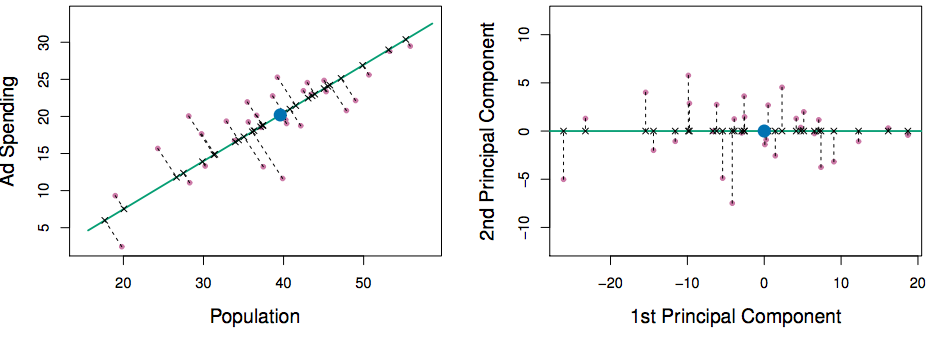
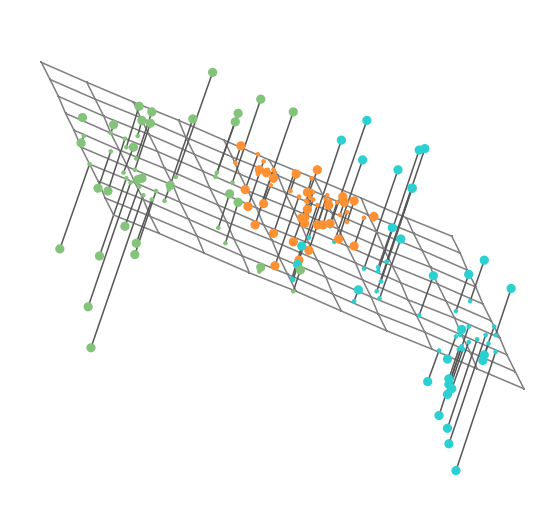
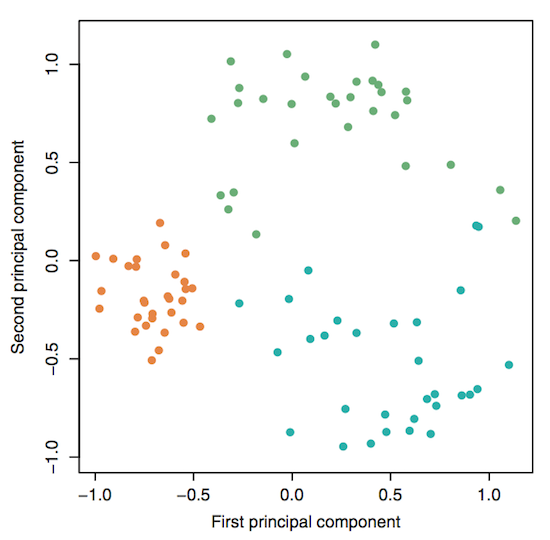
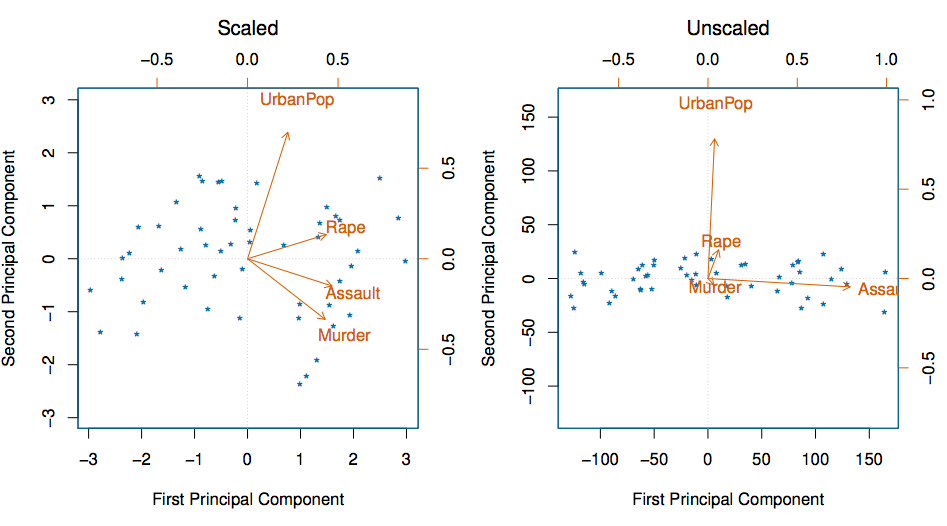
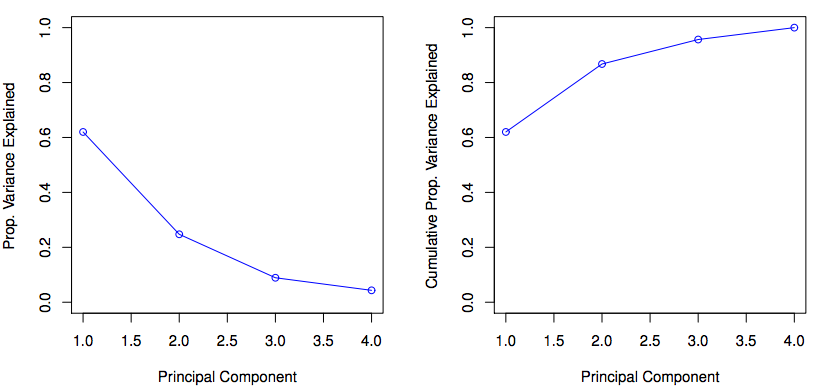
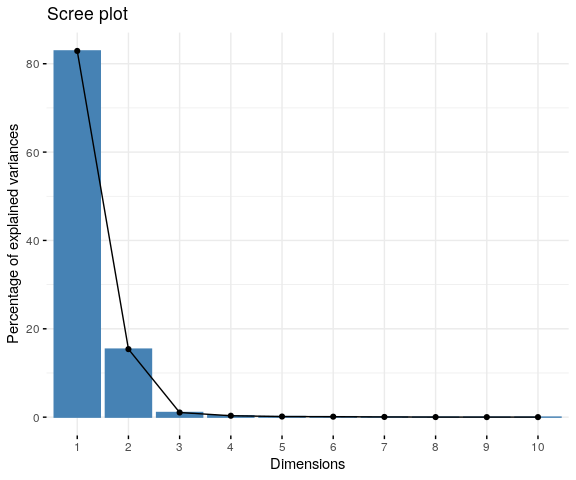
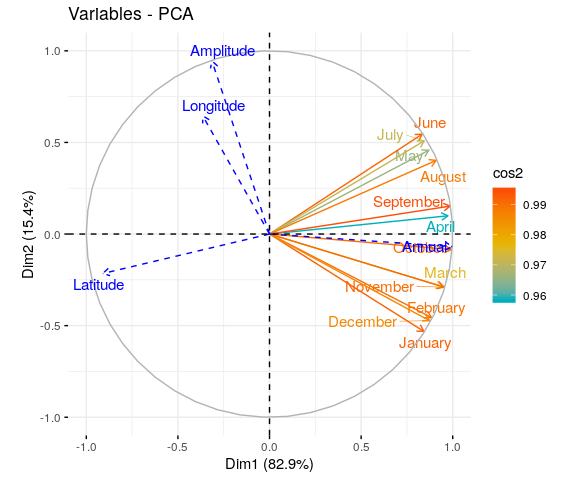
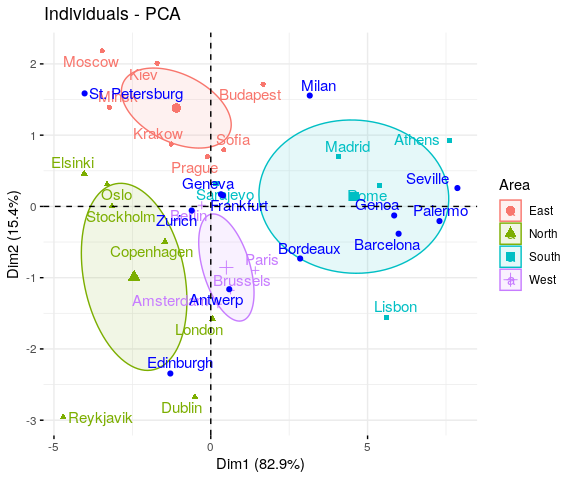
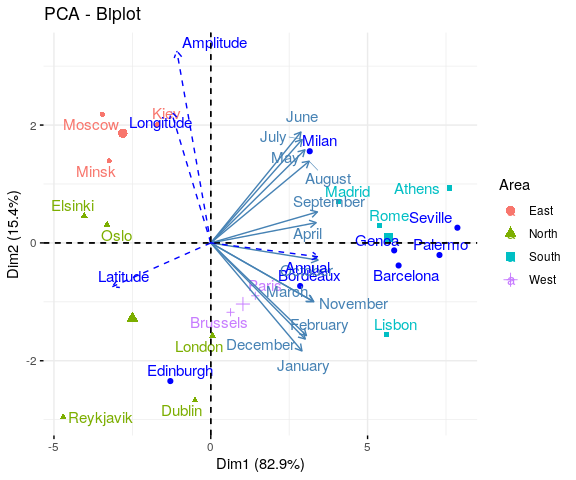
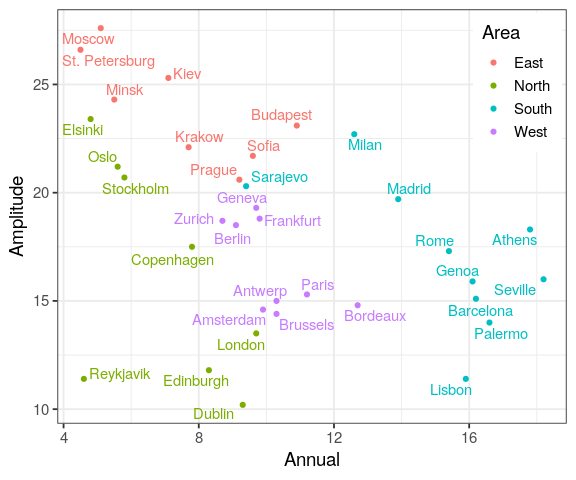
Reading
- Statistics. An introduction using R by Michael J. Crawley. In particular Chapter 12.

- Biostatistic Design and Analysis Using R by Murray Logan (free pdf). In particular Chapter 10.

- Extending the Linear Model with R by Julian Faraway. In particular Chapter 8.